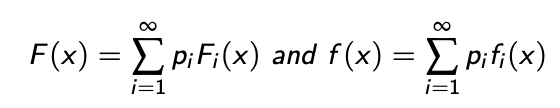Random variable can be generated from a good random number generator. If real variables has moved the reality, we could design a future with a good random variables.
Author: Minkyu Choi
Last updated: 07/19/2019
Inverse Transform Method
Inverse transform sampling is a method for generating random numbers from any probability distribution by using its inverse cumulative distribution F−1(x)F−1(x). Recall that the cumulative distribution for a random variable XX is FX(x)=P(X≤x)FX(x)=P(X≤x). In what follows, we assume that our computer can, on demand, generate independent realizations of a random variable UU uniformly distributed on [0,1]
Cutpoint Method
This inverse-transform method has the advantage of having an optimal O(n) setup time. However, the average number of steps required to sample X is not optimal, and if several samples of X are needed, then the cutpoint method offers an average number of two comparison steps needed to sample an observation, yet still has an O(n) initial setup time
Without loss of generality, we can assume that X = [1, n]. Also, let qi = P(X ≤ i). Then the idea behind the cutpoint method is to choose m ≥ n, and define sets Q1, . . . , Qm for which
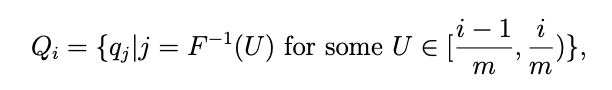
for all i = 1, . . . , m. In words, the unit interval [0, 1] is partitioned into m equal sub-intervals of the form $[\frac{(i−1)} m, \frac{i}m)$, i = 1, . . . , m. And when U falls into the i th sub-interval, then Qi contains all the possible qj values for which F −1 (U) = j. That way, instead of searching through all of the q values, we save time by only examining the qj values in Qi , since these are the only possible values for which $F^{-1} (U) = j$.
Convolution Method
- Sum of n variables: $x = y_1 + y_2 + … y_n$
- Generate n random variate yi’s and sum
- For sums of two variables, pdf of x = convolution of pdfs of y1 and y2. Hence the name
- Although no convolution in generation
- If pdf or CDF = Sum ⇒ Composition
- Variable x = Sum ⇒ Convolution
Acceptance-Rejection Method
Finding an explicit formula for F −1 (y) for the cdf of a rv X we wish to generate, F(x) = P(X ≤ x), is not always possible. Moreover, even if it is, there may be alternative methods for generating a rv distributed as F that is more efficient than the inverse transform method or other methods we have come across. Here we present a very clever method known as the acceptance-rejection method.
Composition Method
Can be used when m can be expressed as a convex combination of other distributions Fi , where we hope to be able to sample from $F_i$ more easily than from F directly.